Lesson 2: Spontaneity and Entropy

Part d: The Second Law of Thermodynamics

Part a: Driving Forces for Change
Part b: What is Entropy?
Part c: Mathematics of Entropy Change
Part d: The Second Law of Thermodynamics

 

The Big Idea

Spontaneous changes are driven by the spread of matter and energy. The Second Law of Thermodynamics associates the entropy changes of both the system and the surroundings to matter spread and energy spread, providing a reliable means of predicting whether a process will occur spontaneously.

 

The Second Law of Thermodynamics

In Lesson 2a, it was stated that energy spread and matter spread are the two driving forces for spontaneous processes. Nature favors processes that spread energy as widely as possible and spread matter as widely as possible. The question now arises: How do the concepts of energy spread and matter spread relate to entropy and its connection to spontaneity? The best answer to this question lies in a thorough understanding of the second law of thermodynamics:

 
 
 

The Universe, The System, and The Surroundings

It is important to note that the second law of thermodynamics makes the claim that all spontaneous processes increase the entropy of the universe. The emphasis here is on universe. The universe includes the chemical system that is under study and everything else outside of the system. This everything else is referred to as the surroundings. Put another way, we can write:

Universe   =   System   +   Surroundings

 

The second law does not claim that the entropy of the system must increase. And it does not claim that the entropy of the surroundings must increase. The second law claims that the net entropy - that of the system AND the surroundings - must increase. The fact is that many processes are spontaneous that have a decrease in a system’s entropy. Liquid water turning to ice in the freezer is an example of a spontaneous change that results in an entropy decrease within the system (the water). But even though the system decreases its entropy, the process is still spontaneous (at temperatures below 0°C) since it is accompanied by an even greater increase in entropy in the surroundings. The rule is:

∆S_system   +   ∆S_surroundings   >   0
 

 

 

 

The Entropy Change of Surroundings

Lesson 2c discussed a method for determining the entropy change of a system undergoing a chemical or physical change. We have not yet discussed the entropy change of the surroundings. The entropy of the surroundings is primarily affected by the flow of energy from or to the surroundings. When heat flows from the system to the surroundings (as in an exothermic reaction), the temperature of the surroundings increases. The particles in the surroundings increase their random motion and the entropy of the surroundings increases. On the other hand, a flow of heat from the surroundings to the system (as in an endothermic reaction) lowers the temperature of the surroundings. The random motion of particles decreases and the entropy of the surroundings decrease.

 
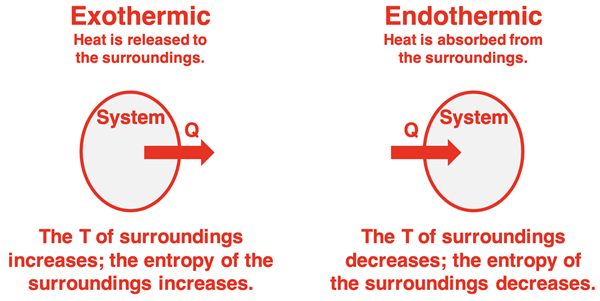
When the system has a negative enthalpy change (∆H_system) - an exothermic process - there is an equal quantity of heat (Q) released to the surroundings. The entropy of the surroundings changes; it increases The actual change is calculated using the equation:

where T is the Kelvin temperature. The negative sign in the equation ensures that the surroundings have a positive ∆S (increase in entropy) when there is a negative ∆H value (an exothermic process).
 
The same equation and a similar line of reasoning can be applied to endothermic processes for which the system’s enthalpy change is a positive value. When heat enters the system from the surroundings, the ∆H value is positive. Because of the negative sign on the right side of the equation, the ∆S_surroundings value is negative. The same equation predicts that the surroundings decrease their entropy for endothermic processes.
 
The following table summarizes these ideas.

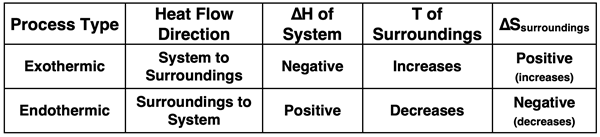
Exothermic processes cause the entropy of the surroundings to increase. If spontaneity requires that the entropy of the universe increases, then exothermic processes are more likely to be spontaneous than endothermic processes. This is one of the two driving forces for spontaneous processes.

 
 

Temperature Effects

The effect of the system’s enthalpy change upon the entropy change of the surroundings is not the same for all temperatures. The equation for the ∆S_surroundings (above) has a Kelvin temperature in the denominator. For the same enthalpy change, the entropy change of the surroundings will be greatest at lower temperatures and smallest at higher temperatures.
 

 
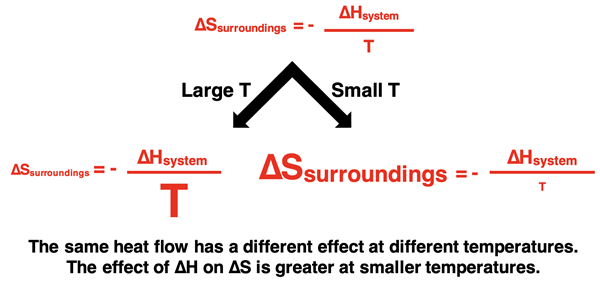
To illustrate this idea, consider the following analogy. Giving $500 to a billionaire will have an insignificant impact upon their net worth. A billionaire has LOTS of money and the additional $500 cash flow is hardly noticeable. But if $500 is given to a high school student, the impact would be enormous. It is the same $500 that the billionaire received, but the effect of the cash flow is quite noticeable since the high school student has very little money. In the same way, if the surroundings are at a high temperature, a flow of 500 kJ of heat will increase the kinetic energy of its particles. But since they are already at high energy, the addition is hardly noticeable. It is a small fraction of the energy that it already has. Yet the effect of the 500 kJ of heat flow on low temperature particles is quite noticeable. It is the same heat flow in each situation, but the impact is more noticeable for low-temperature surroundings.
 
 
 

Spontaneity and Entropy

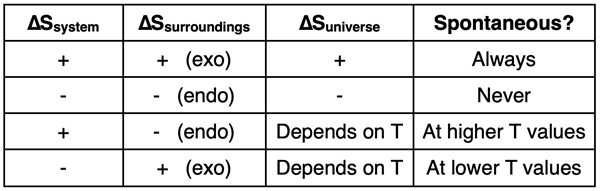
As we end Lesson 2, we can claim that spontaneous processes are those that increase the entropy of the universe. This means that the sum of the ∆S_system and ∆S_surroundings must be positive. There are three possibilities to consider:

• If both ∆S_system and ∆S_surroundings are positive, then the process is guaranteed to be spontaneous at any temperature.
• If both ∆S_system and ∆S_surroundings are negative, then the process is guaranteed to not be spontaneous at any temperature.
• If one but not both of the ∆S_system and ∆S_surroundings are positive, then the spontaneity of the process will be dependent upon temperature. The effect of ∆S_surroundings will be maximized at lower temperatures and minimized at higher temperatures. If ∆S_surroundings is positive (and ∆S_system is negative), then the process will be spontaneous in a lower temperature range. But if ∆S_surroundings is negative (and ∆S_system is positive), then the process will be spontaneous in a higher temperature range.

 

 
If you began Lesson 2 on the first page (see Driving Forces for Change), then you might recognize that the entropy change of the system is most closely associated with matter spread. The diffusion of a gas, the change of a liquid to a gas, and the dissolving of a solid in solution are clear examples of matter spread. These processes provide particles with more freedom of movement and more possible arrangements (microstates). Matter spread results in positive entropy changes and thus contributes to an increase in the entropy of the universe.
 
You might also recognize that the entropy change of the surroundings is most closely associated with energy spread. Exothermic processes release energy from where it is concentrated within the system to the vast surroundings. This increases the entropy of the surroundings and thus contributes to an increase in the entropy of the universe.
   
While both matter spread and energy spread can occur in both the system and surroundings, the system’s entropy change is often dominated by matter spread. And the entropy change of the surroundings is dominated by energy spread (heat flow). We see in the second law of thermodynamics the two driving forces - matter spread (∆S_system) and energy spread (∆S_surroundings).
   
 

It is often bothersome to students to read statements like the spontaneity depends on T or the process is spontaneous at lower T values. We don’t blame you if you’re bothered because there is something missing in such statements. Details! Details like what is meant by lower T values or higher T values or in what way does the spontaneity depend on T. But the fact is that those details are coming. In Lesson 3 we will introduce a state function known as Gibb’s free energy and an associated equation that allows one to calculate the threshold temperature above which or below which a process is spontaneous. But before you leave, try one or more the suggestions in the section below to reinforce the ideas in this lesson.
 
 
 

Before You Leave - Practice and Reinforcement

Now that you've done the reading, take some time to strengthen your understanding and to put the ideas into practice. Here's some suggestions.
 

• Try our Concept Builder titled Spontaneity and Driving Forces. Any one of the three activities provides a great follow-up to this lesson.
• The Check Your Understanding section below includes questions with answers and explanations. It provides a great chance to self-assess your understanding.
• Download our Study Card on The Second Law of Thermodynamics. Save it to a safe location and use it as a review tool. (Coming Soon.)

 
 
 

Check Your Understanding of the Second Law of Thermodynamics

Use the following questions to assess your understanding of the second law and associated concepts from Lesson 2. Tap the Check Answer buttons when ready.
 
1. Identify the following statements as being TRUE or FALSE:

1. Exothermic processes are always spontaneous. 
   
   Check Answer
   Answer: FALSE
   
   Exothermic processes can be non-spontaneous. While being exothermic is a favorable condition, there is a second driving force that must be considered - the entropy change of the system. 
   
    
   
    
2. Endothermic processes are never spontaneous. 
   
   Check Answer
   Answer: FALSE
   
   Endothermic processes can be spontaneous. While being endothermic is not a favorable condition, there is a second driving force that must be considered - the entropy change of the system. 
   
    
   
    
3. Exothermic processes cause the entropy change of the surroundings to be positive. 
   
   Check Answer
   Answer: TRUE
   
   Exothermic process release heat into the surroundings. This increases the temperature and average kinetic energy of the particles of the surroundings. Having a greater kinetic energy, the entropy of the surroundings increases. 
   
    
   
    
4. A positive change in entropy means an increase in entropy. 
   
   Check Answer
   Answer: TRUE
   
   When you learn that a reaction has a positive ∆S value, then you know there is an increase in S (entropy). Positive changes for a quantity always indicate increases in that quantity.
   
    
   
    
5. The second law of thermodynamics states that every spontaneous process results in an increase in entropy of the system. 
   
   Check Answer
   Answer: FALSE
   
   The second law states that spontaneous processes are those for which the entropy change of the universe is positive. The ∆S of both the system and the surroundings must be considered.
   
    
   
    
6. Endothermic processes release energy to the surroundings and lead to more energy spread. 
   
   Check Answer
   Answer: FALSE
   
   An exothermic process releases energy to the surroundings and results in energy spread. Endothermic processes do the opposite.
   
    
   
    
7. Processes with a negative enthalpy change (of the system) and a positive entropy change of the system are always spontaneous. 
   
   Check Answer
   Answer: TRUE
   
   An exothermic process increases the entropy of the surroundings. Since the entropy of the system also increases, the process is spontaneous at all temperatures.
   
    
   
    
8. Processes with a negative entropy change of the surroundings and a positive entropy change of the system are more likely to be spontaneous at low temperatures than at high temperatures. 
   
   Check Answer
   Answer: TRUE
   
   This is the case where there are two competing driving forces. The ∆S_system is a favorable condition. The ∆S_surroundings is a non-favorable condition. At relatively high temperatures, the impact of ∆S_surroundings is minimized and the reaction will be spontaneous.
   
    
   
    

 
 
2. For an exothermic process with a ∆H_system of -500 kJ, ...

1. ... calculate the ∆S_surroundings at a temperature of 100 K. 
   
   Check Answer
   Answer: +5.00 kJ/K or +5000 J/K
   
   ∆S_surroundings = -1•∆H_system / T
   
   ∆S_surroundings = -1•(-500 kJ) / 100 K
   
   ∆S_surroundings = +5.00 kJ/K or +5000 J/K
   
    
   
    
2. ... calculate the ∆S_surroundings at a temperature of 1000 K. 
   
   Check Answer
   Answer: +0.500 kJ/K or +500 J/K
   
   ∆S_surroundings = -1•∆H_system / T
   
   ∆S_surroundings = -1•(-500 kJ) / 1000 K
   
   ∆S_surroundings = +0.500 kJ/K or +500 J/K
   
    
   
    
3. Describe the effect of temperature upon the entropy change of the surroundings. 
   
   Check Answer
   Answer:
   As can be seen in the data, temperature reduces the effect that an enthalpy change has upon the entropy change of the surroundings. The entropy change of the surroundings is 10 times greater at the lower temperature (100 K) than it is at the higher temperature (100 K).
   
    
   
    

 
 
3. Consider the following change of state:
Identify the sign (+ or -) on the following quantities:
 
∆S_system:
∆H_system:
∆S_surroundings:



This process is _____.

1. spontaneous at all temperatures
2. not spontaneous at any temperatures
3. spontaneous only at relatively high temperatures
4. spontaneous only at relatively low temperatures

 


 
4. Consider the following exothermic reaction:
 
Identify the sign (+ or -) on the following quantities:
 
∆S_system:
∆H_system:
∆S_surroundings:



This process is _____.

1. spontaneous at all temperatures
2. not spontaneous at any temperatures
3. spontaneous only at relatively high temperatures
4. spontaneous only at relatively low temperatures

 
5. Consider the following combustion reaction:
  Identify the sign (+ or -) on the following quantities:
 
∆S_system:
∆H_system:
∆S_surroundings:



This process is _____.

1. spontaneous at all temperatures
2. not spontaneous at any temperatures
3. spontaneous only at relatively high temperatures
4. spontaneous only at relatively low temperatures

 
6. Consider the following endothermic decomposition reaction:
 
Identify the sign (+ or -) on the following quantities:
 
∆S_system:
∆H_system:
∆S_surroundings:



This process is _____.

1. spontaneous at all temperatures
2. not spontaneous at any temperatures
3. spontaneous only at relatively high temperatures
4. spontaneous only at relatively low temperatures

 
 

 
 



Jump to Next Lesson: Predicting Spontaneity with Gibbs Free Energy

View: Chapter Contents